Estimation of Maximum Sustainable Yield Using Production Modeling: A Stock Appraisal of Indian Oil Sardine (Sardinella longiceps) from Pakistani Waters

Abdul Baset1, Qun Liu1,*, Muhammad Tariq Hanif1, 2, Baochao Liao1, Aamir Mahmood Memon1,3 and Muhammad Mohsin1

1College of Fisheries, Ocean University of China, Qingdao 266003, China

2Marine Fisheries Department, Fish Harbor West Wharf, Karachi 74000, Pakistan

3Sindh Fisheries Department, Hyderabad 71000, Sindh, Pakistan

ABSTRACT

Time series of catch and effort data were analyzed to estimate the Maximum Sustainable Yield (MSY) of Indian oil sardine, Sardinella longiceps (Valenciennes, 1847, Family: Clupeidae), fishery resources from Pakistani waters. The catch and effort data (1994 – 2009) were analyzed by CEDA (catch and effort data analysis) consists of Fox, Schaefer and Pella Tomlinson models and ASPIC (a surplus production model incorporating covariates) contain Fox and Logistic models. The average annual landings of S. longiceps stocks were 38 353 t while the highest and lowest 65 050 t in 1994 and 26 937 t in 2009 was recorded correspondingly. The MSY was estimated using the initial proportion (IP) value of 1 because the starting catch was approximately 100% of the maximum catch. The estimated values of MSY using CEDA with the Fox model under three error assumptions of normal, log-normal and gamma were 25 860.07 t (R2 = 0.864), 26 812.65 t (R2 = 0.836) and 26 665 t (R2 = 0.85), respectively. The MSY values with Schaefer and Pella Tomlinson models under two error assumptions normal and log-normal were 29 160.13 t (R2 =0.84) and 30 455.5 t (R2 =0.807), respectively. The values of Schaefer and Pella Tomlinson models were the same. The gamma error assumption showed minimization failures for Schaefer and Pella Tomlinson models. The estimated values of MSY using ASPIC computer software with two surplus production models of Fox and logistic were 28 180 t (R2 =0.915) and 33 260 t (R2 =0.897) respectively. The estimated values of MSY from CEDA were about 26 000 - 31 000 t and from ASPIC were 29 000 - 31 000 t. The estimated MSY values of CEDA and ASPIC were higher than the most recent catch. This shows that the stocks are in a safe condition.

Article Information

Received 29 January 2016

Revised 26 April 2016

Accepted 03 August 2016

Available online 02 February 2017

Authors’ Contributions

QL conceived and designed the study. MTH arranged the data. BL and AMM helped in data analysis. MM prepared the Figures. AB analyzed the data and wrote the article. QL reviewed and edited the article.

Key words

Sardinella longiceps, Maximum sustainable yield, Catch and effort data analysis (CEDA), A surplus production model incorporating covariates (ASPIC), Pakistan.

* Corresponding author: [email protected]

0030-9923/2016/0004-1161 $ 8.00/0

Copyright 2016 Zoological Society of Pakistan

DOI: http://dx.doi.org/10.17582/journal.pjz/2017.49.2.521.528

INTRODUCTION

 

Fisheries resources are not only playing a significant role in the national economy, but also take part in the human development and welfare, such as in terms of providing a quality source of food and employment with the major aspect of self-renewable in nature. Therefore, if the fish stocks were managed in a sustainable manner then their effects can be limitless (WHO/FAO, 2003).

The coastal belt of Pakistan is about 1,120 km long from the southeast Indian border to the northwest Iranian border (Fig. 1) with an EEZ (exclusive economic zone) of 240,000 km2 with an additional continental shelf area of about 50,270 km2. The EEZ of the country is rich in fish and mineral resources (FAO, 2009). There were about 250 commercially important demersal fishes (Bianchi, 1985), 50 small pelagic, 15 medium-sized pelagic and 20 large pelagic fish species in Pakistani water (FAO, 2009). Small pelagic fishes have a cosmopolitan distribution in the world seas. These species were caught, canned and consumed globally (Lanier, 1981). These resources mainly include species from family Clupeidae, Engraulidae, Scomboridae and Carangidae. Indian oil sardine (Sardinella longiceps Valenciennes, 1847) belongs to the family Clupeidae and local names are Tarli, Luar in Sindhi and Lugger, Luar in Baluchi language (Bianchi, 1985). Body length has estimated about15-17 cm at the end of first year and 19 cm at the end of second year (Hornell, 1924). Its maximum length is 23 cm and commonly 16 cm in Pakistan (Bianchi, 1985).

 

 

Oil sardine, S. longiceps is a valuable commercial fish, used for food as well as for the production of fishmeal and oil (Deshmukh et al., 2010). Several studies are related on the biological and ecological aspects of Indian oil sardine (John and Menon, 1942; Nair, 1949, 1959; Antony, 1964).

In the present paper we analyzed the catch and effort data of S. longiceps from Pakistan to estimate maximum sustainable yield (MSY). Several surplus production models have been used to appraise the fish stocks for the estimation of MSY (e.g. Pitcher and Hart, 1982; Hilborn and Walters, 1992; Prager, 1994; Walter and Perma, 1996; Quinn and Deriso, 1999; Maunder et al., 2006). These models express the fishery yields as a function of catch and fishing effort. Some work has already been done on the estimation of MSY of various fish species from Pakistan and China (e.g. Panhwar et al., 2012a, b; Kalhoro et al., 2013; Siyal et al., 2013; Wang and Liu, 2013).

The aim of this article is to provide baseline information on the current stock status of Indian oil sardine (S. longiceps) in Pakistani waters. For this purpose, we estimated the MSY biological reference points from a variety of surplus production models (Schaefer, 1954; Fox, 1970; Pella and Tomlinson, 1969) with different error assumptions by catch and effort data analysis (CEDA) (Hoggarth et al., 2006) and a non-equilibrium surplus production model ASPIC (a surplus-production model incorporating covariates, Prager, 2005) software. The estimated values may help to draw the desired fisheries regulations for the sustainable utilization of this fishery resource in the country.

 

Table I.- The catch and effort data of Sardinella longiceps fishery in Pakistani waters from 1994-2009 (taken from the handbook of fisheries statistics of Pakistan).

Year	Catch	Effort	CPUE
1994	65050	10296	6.317988
1995	55177	11066	4.986174
1996	52290	11061	4.727421
1997	51930	10983	4.728216
1998	44079	11444	3.851713
1999	30629	11768	2.602736
2000	31167	12114	2.572808
2001	33319	12618	2.640593
2002	29815	12695	2.348562
2003	32939	12838	2.565742
2004	34336	13002	2.640824
2005	31532	13145	2.398783
2006	30955	13308	2.326044
2007	31282	13426	2.329957
2008	32213	13522	2.382266
2009	26937	13879	1.940846

Note: Catch is in the form of metric ton.

 

MATERIALS AND METHODS

Data source

The catch and effort data of Indian oil sardine (Sardinella longiceps) for the period of 1994 to 2009 (16 years) were from the handbook of Fisheries Statistics of Pakistan compiled by Marine Fisheries Department (MFD), Karachi, Pakistan (Table I). Fishing effort is presented by the number of operational fishing boats in the maritime region of Pakistan, and the per annum total catch is presented in the form of catch weight (metric tons).

Surplus production models

The fishery statistics of S. longiceps were analyzed by CEDA and ASPIC. In order to minimize the biasness in the results we used both of them which were developed by fisheries scientists from UK and US. Both have some technical differences but they are based on the same theory. There were three surplus production models (SPMs) also called biomass dynamic models (BDMs) used in CEDA package i.e. Schaefer, Fox and Pella-Tomlinson. The most commonly used model is Schaefer (1954) which is based on the logistic population growth model:

 

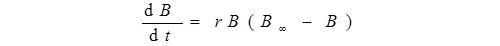
Then, Fox (1970) proposed a study based on the Gompertz population growth equation:

 

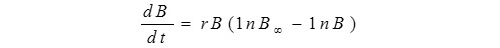
Pella and Tomlinson (1969) proposed the use of a generalized production equations.

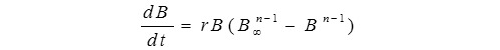
Where B is fish stock biomass, t is time, B∞ is carrying capacity, and r is intrinsic rate of population increase. CEDA, version 3.0.1 (Hoggarth et al., 2006).

CEDA is a pc-based software package, designed by fishery scientists in UK for fish stock assessments, which was first developed in 1992 and has been adjusted and further developed on request of users.

CEDA, version 3.0.1 includes three non-equilibrium surplus production models (Schaefer, 1954; Fox, 1970; Pella and Tomlinson, 1969) with three error assumption (normal, log-normal and gamma). The computer package can calculate the following key parameters: MSY, q (catchability coefficient), K (carrying capacity), r (intrinsic growth rate), replacement yield, final biomass, whereas CV (coefficient of variation) of the estimated MSY values can also be calculated. The package requires an input value of initial biomass (B1) over the carrying capacity by the user. When the IP (initial proportion) value has set to zero, it points out that the fishery started from a virgin population and if the IP value is close to 1, it indicates that the fishery initiate from a heavily harvested population. However, in some cases starting biomass is fixed by programmer i.e.

B1=K

ASPIC, version 5.0 (Prager, 2005)

ASPIC is a non-equilibrium application of the surplus production models which was developed by a fishery scientist in USA and started in 1994 and is freely available from the internet. The model is more formally described in Prager (1994) and Quinn and Deriso (1999).

ASPIC package contains two surplus production models Logistic (Schaefer) and Fox (a special case of GENFIT). At the beginning, the program was based on the logistic model (Scheafer, 1954) but the most current version 5.0 allows the selection criterion between logistic and generalized production models. The main output parameters are: MSY, q, K, ratio of starting biomass over carrying capacity (B1/K), coefficient of determination (R2), coefficient of variation (CV), stock biomass giving MSY (BMSY), and fishing mortality rate at MSY (FMSY).

 

RESULTS

CEDA results

CEDA is a computer program which requires catch and effort data with three non-equilibrium surplus production models and three error assumptions (Hoggarth et al., 2006). The average catch of S. longiceps from Pakistani waters in the 16-year period of 1994 – 2009 was 38,353 t. Table I shows that the observed catch in 1994 was 65,050 t which was the highest catch while in 2009 it was 26,937 t which was the lowest catch. In Tables II and III, bootstrapping confidence limit method was used for obtaining the CV. The results from the CEDA package are highly responsive to the input IP (initial proportion) values (Table II). The estimated values of MSY were different when IP from 0.1 to 1. Table III showed the CEDA results with IP of 1 because the initial yield was about 100% of the maximum catch. The estimated values of MSY with CV from the Fox model with three error assumptions (normal, log normal and gamma) were produced at 25,860 t (CV = 0.060), 26,812 t (CV = 0.064) and 26,665 t (CV = 0.051), respectively. Similarly, the estimated values of MSY for Schaefer and Pella Tomlinson with two error assumptions normal and log normal were 29,160 t (CV = 0.101), (CV=0.088) and 30,455 t (CV = 0.084), (CV=0.092) respectively. The Fox model produced R2 = 0.864, 0.836 and 0.85, respectively, whereas Schaefer and Pella Tomlinson models produced R2 =0.84 and 0.807, respectively. The values of MSY were the same from Schaefer and Pella Tomlinson. Gamma error assumption showed minimization failure for Schaefer and Pella Tomlinson. There was a little difference among the estimated values of MSY from all models, i.e. Fox, Schaefer and Pella Tomlinson while estimated R2 values show a better fit to the data.

 

Table II.- Estimates of MSY values for the S. longiceps fishery (Coefficient of variation is in brackets) using CEDA computer package with the initial proportion ratio from 0.1 to 1.

IP	Models
	Fox				Schaefer				Pella Tomlinson
	Normal	Log- normal	Gamma		Nor mal	Log-normal	Gam ma		Nor mal	Log-normal	Gam ma
0.1	3.10E+1	68493.15	MF		MF	144728	MF		MF	144728	MF
	(0.7842)	(0.02017)	MF		MF	(0.0002)	MF		MF	(0.000)	MF
0.2	275047	49003.98	282050		MF	78654.3	MF		MF	78654	MF
	(0.006)	(0.01711)	(0.126)		MF	(0.0003)	MF		MF	(0.004)	MF
0.3	46451.3	49499.8	17118		410649	56331.2	5701		4106	56331	57015
	(0.024)	(0)	(693.6)		(0.0443)	(0.0017)	(0.0)		(0.04)	(0.001)	(0.007)
0.4	39144	43848.73	MF		197787	53320.9	MF		19778	53320	MF
	(0.048)	(2.34E- 05)	MF		(5688.9)	(4.74E- 05)	MF		(7473)	(6.7E- 05)	MF
0.5	34705.8	40285.73	35621		MF	40699.9	MF		MF	40699	MF
	(0.062)	(0.0052)	(0.058)		MF	(0.0105)	MF		MF	(0.011)	MF
0.6	31779	31036.6	MF		215805	43660	MF		21580	43660	MF
	(0.056)	(0.0585)	MF		(42471)	(0.0007)	MF		(4846)	(0.000)	MF
0.7	29749.2	30891.99	MF		40805.9	41691	425		40806	41691	42567
	(0.050)	(553563)	MF		(0.0281)	(0.000)	(0.0)		(0.028)	(0.001)	(0.015)
0.8	28310.3	29442.22	MF		35581.8	40498.	MF		35582	40498	MF
	(0.057)	(0.06694)	MF		(0.0790)	(0.0035)	MF		(0.074)	(0.003)	MF
0.9	27279	28441.98	33462		31862.5	31523	334		31863	31523	33498
	(0.057)	(0.06225)	(1370)		(0.0992)	(0.070)	(0.0)		(0.099)	(0.073)	(0.102)
1	26550.8	27504.57	27351		29160	30455.5	MF		29160	30455	MF
	(0.060)	(0.06156)	(0.05)		(0.1013)	(0.084)	MF		(0.08)	(0.092)	MF

MF, showing minimization failures.

 

Table III.- Application of computer package CEDA (catch and effort data analysis) for S. longiceps fishery in Pakistan to estimate MSY and other parameters, using IP (initial proportion) of 1.

Models	K	r	MSY	Ryield	CV	q	R2	Biomass
Fox (Normal)	345402.3	0.208952	26550.79	25860	0.0601	2.03E-05	0.864	99206.46
Fox (Log normal)	322858	0.231573	27504.57	26812	0.0643	2.22E-05	0.836	93147.27
Fox (Gamma)	326674	0.227593	27351.31	26665	0.0517	2.19E-05	0.85	94289.3
Schaefer (Normal)	290645.5	0.401315	29160.13	22656	0.1013	2.46E-05	0.84	76692.88
Schaefer (Log normal)	268659.6	0.453444	30455.5	23880	0.08494	2.70E-05	0.807	71915.17
Schaefer (Gamma)	MF	MF	MF	MF	MF	MF	MF	MF
Pella Tomlinson (Normal)	290645.5	0.401315	29160.13	22656.	0.0884	2.46E-05	0.84	76692.88
Pella Tomlinson (Log normal)	268659.6	0.453444	30455.5	2388	0.0921	2.70E-05	0.807	71915.17
Pella Tomlinson (Gamma)	MF	MF	MF	MF	MF	MF	MF	MF

Note: MF stands for minimization failure.

The parameters are: K, carrying capacity; r, intrinsic population growth rate; MSY, maximum sustainable yield; Ryield, replacement yield; CV, Coefficient of variation; q, catchability coefficient; R2, coefficient of determination and biomass.

 

 

Figure 2 showed the estimated and observed catches, when using the IP value of 1, the observed catches from all models were approximately near to the estimated catch.

ASPIC results

ASPIC (Prager, 2005) was also used for the estimation of MSY and related parameters of the Indian oil sardine fishery from Pakistani waters. Results from the non-equilibrium surplus production models of Logistic and Fox in ASPIC computer package are shown in Table IV. The IP was 1, because the initial yield was about 100% of the maximum catch. The estimated values of MSY from Fox and logistic with CV were 28,180 t (CV=0.039) and 33,260 t (CV=0.084), respectively. The rate of fishing mortality at MSY (FMSY) and stock biomass giving MSY (BMSY) model was 0.268 and 105,100 t from the Fox and 0.329 and 100,900t from the Logistic model correspondingly, while the estimated values of K (carrying capacity) in the Fox model were a little higher than in the Logistic model. In addition to this, Table V shows ASPIC results for the

 

Table IV.- ASPIC computer program results with IP (initial proportion) at 1 for S. longiceps, fishery from Pakistani waters to estimate MSY and other parameters.

Model	IP	MSY	B1/K	K	q	Fmsy	R2	CV	Bmsy
FOX	1	28180	1.01E+00	2.86E+05	2.52E-05	2.68E-01	0.915	0.039191	105100
LOGISTIC	1	33260	9.99E-01	2.02E+05	3.81E-05	3.30E-01	0.897	0.084747	100900

MSY, maximum sustainable yield; B1/K, starting biomass over carrying capacity; K,carrying capacity; FMSY , fishing mortality rate at MSY; q, catchability coefficient; BMSY, stock biomass giving MSY; R2, coefficient of determination.

 

Table V.- ASPIC results for the S. longiceps fishery in Pakistan with the initial proportion (IP) ranging from 0.1 to 1.

Model	IP	MSY	B1/K	K	q	Fmsy	R2	CV	Bmsy
	0.1	52020	3.15E -0	2.23E +05	1.22E-04	6.33E-01	0.813	25.10636	82190
	0.2	34800	5.57E -0	2.93E +05	4.51E-05	3.23E-01	0.907	0.229254	107700
	0.3	28180	1.01E +0	2.86E +05	2.52E-05	2.68E-01	0.915	0.036071	105200
	0.4	28180	1.01E +0	2.86E +05	2.52E-05	2.68E-01	0.915	0.035486	105200
FOX	0.5	47340	3.11E-01	3.31E +05	7.14E-05	3.89E-01	0.909	0.08287	121600
	0.6	35740	5.26E-01	2.96E +05	4.72E-05	3.28E-01	0.907	0.277031	108900
	0.7	28180	1.01E +0	2.86E +05	2.52E-05	2.68E-01	0.915	0.034121	105200
	0.8	28180	1.01E +0	2.86E +05	2.52E-05	2.68E-01	0.915	0.04855	105100
	0.9	28180	1.01E +0	2.86E +05	2.52E-05	2.68E-01	0.915	0.039971	105100
	1	28180	1.01E +0	2.86E +05	2.52E-05	2.68E-01	0.915	0.039191	105100
	0.1	92120	2.29E-01	1.12E+ 05	2.45E-04	1.65E+00	0.936	0.006024	55760
	0.2	76550	3.01E-01	9.07E +04	2.43E-04	1.69E+00	0.964	0.007178	45360
	0.3	47340	5.76E-01	1.54E +05	8.07E-05	6.17E-01	0.917	1.706848	76790
	0.4	45470	6.61E-01	1.39E +05	8.38E-05	6.57E-01	0.909	0.023926	69250
LOGISTIC	0.5	48720	4.95E-01	1.96E +05	6.73E-05	4.96E-01	0.903	0.051878	98180
	0.6	49080	5.16E-01	1.71E +05	7.71E-05	5.73E-01	0.915	2.51574	85590
	0.7	46080	6.53E-01	1.35E +05	8.76E-05	6.84E-01	0.91	10.11523	67360
	0.8	45310	6.55E-01	1.43E +05	8.16E-05	6.36E-01	0.91	0.031893	71270
	0.9	46870	6.19E-01	1.39E +05	8.73E-05	6.76E-01	0.915	7.574493	69340
	1	33260	9.99E-01	2.02E +05	3.81E-05	3.30E-01	0.897	0.084747	100900

The meaning of the parameters same as in Table IV.

 

S. longiceps fishery in Pakistan with IP ranging from 0.1 to 1. The program does not show higher sensitivity to initial proportion values as compared to CEDA computer package. The MSY values of Logistic model were high when IP = 0.1 and 0.2, the remaining were between 28,000 t to 50,000 t from both Fox and Logistic models which were relatively close to the annual catch of an Indian oil sardine fishery. The Fox model produced R2 =0.915 while Logistic produced R2 =0.897, which were higher than those from the CEDA computer package and showed the excellent fitting to the data.

 

DISCUSSION

 

Decisions derived to manage the fisheries are commonly directed by the stock assessment results. Therefore, it is essential that scientists provide a reliable description of stock dynamics and stock status to the managers (Lynch et al., 2012). The main purpose of the paper was to estimate the MSY of S. longiceps by Surplus Production models. The results obtained from CEDA and ASPIC in this study were basically consistent among the three surplus production modeling approaches i.e. Fox, Schaefer and Pella Tomlinson. Logistic approach resulted in a higher value of MSY which showed that the Fox model is more conservative.

 

Modeling approach

Catch-per-unit-effort (CPUE) is considered to be proportional to the fish population abundance and referred as the relative abundance index. Several population dynamic models were used to predict the relative abundance index in order to obtain the future values of predicted absolute abundance by multiplying with a constant (catchability coefficient, q) (Hinton and Maunder, 2004). To do so, the SPMs or BDMs are the plausible approach due to their holistic or simple in nature. The surplus production models can determine the level of effort at which a fishery produces a maximum yield of a fish stock in a sustainable manner without changing the long term productivity termed as MSY (Sparre and Venema, 1998).

 

Assumptions, limitations and trends

The perception or understanding of MSY has played a significant role in the fishery science over the decades and often regarded as the target Biological Reference Point (BRPs) (Smith and Punt, 2001), which serve as a standard of measurement of stock status from a biological point of view. These reference points are generally summarized under the three main fish stock dynamic models, i.e., stock-recruit, dynamic pool and production models (Gabriel and Mace, 1999).

Fish stock sizes and distributions can fluctuate widely even in their unexploited state, due to the change in environmental factors and also the interrelationships with other species. Some researchers have indicated that if the surplus production is higher than catch it means the population size is increasing, whereas when the catch is greater than surplus production the population has a decreasing trend. Moreover, when the catch and production were equal, it showed a constant trend in fish population size (Hilborn and Walters, 1992; Prager, 2002; Musick and Bonfil, 2004).

Small pelagic fishes accounted for 33.3% of the total marine fishery resources of Pakistan, including Herrings, Sardines, and Anchovies. During the year 1998, the total biomass and MSY of small pelagic fishes was estimated to be 700,000 and 300,000 t, respectively (SMEDA, 2015). However, previously no work has been reported on the MSY of Indian oil sardine (S. longiceps) separately. To our knowledge, this is the first study to investigate the MSY of sardine fisheries from Pakistani water’s. We have found that the trajectory of stock biomass and exploitation rate remains steady for years 1999-2009 except for few minimization failures only in the gamma error assumption.

 

Tools of analysis

CEDA results

CEDA package is limited to three surplus production models, i.e., Fox, Schaefer, Pella-Tomlinson with three error assumptions, i.e., Normal, Log-Normal and Gamma respectively (Hoggarth et al., 2006) from which we can estimate the MSY, and other related population parameters of fish stocks. It can be used as a supportive tool for fishery management. When we use an initial proportion (IP) ranging from 0.1–1 Table II shows that CEDA package is sensitive to the IP values. When IP values were low, the estimated MSY values were higher and when IP values were high the estimated MSY values were lower (Table II). When the IP was from 0.5 - 1, the estimated MSY values from Fox, Schaefer and Pella-Tomlinson production models were lower than that of observed catch data. To minimize the bias in the data we use IP= 1 because the starting catch was roughly 100% of the maximum catch. The estimated values from CEDA package were 25,860 t, 26,812 t and 26,665 t for the Fox model with three error assumptions normal, log normal and gamma respectively, while 29,160 t and 30,455 t for Schaefer and Pella Tomlinson with two error assumptions normal and log normal, respectively (Table III).

 

ASPIC results

Similarly, the ASPIC (Prager, 2005) was used to estimate the values of MSY and related parameters from time series catch and fishing effort data by non-equilibrium surplus production models. The non-equilibrium surplus production models were often used because the fish stocks were rarely in equilibrium state due to several factors affecting the population size i.e., biology, environment and fishing effort. The MSY values and other parameters of Indian oil sardine fishery from Pakistan were estimated and shown in Table IV which indicates that the ASPIC package is not sensible with IP values. The Fox and Logistic models produced R2 =0.915 and 0.897, respectively. In contrast to CEDA, the ASPIC showed a better fit to the data.

 

CONCLUSION

 

The estimated values of MSY from CEDA package were about 26,000 – 31,000 t and from ASPIC the values were 26,000 - 33,000 t .These values are higher than the recent catches of S. longiceps from Pakistani waters. From the outcome of our investigation, it is possible to conclude that the Indian oil sardine fishery in Pakistan were in managed condition.

 

ACKNOWLEDGEMENTS

 

Abdul Baset acknowledges the Chinese Scholarship Council (CSC) for funding his PhD. degree. This work is supported by the Fundamental Research Funds for the Central Universities (No. 201562030).

 

Statement of conflict of interest

Authors have declared no conflict of interest.

 

REFERENCES

 

Antony, R.B., 1964. Some aspects of spawning biology of Indian oil sardine Sardinella longiceps Valenciennes. Indian J. Fish., 11: 45-120.

Bianchi, G., 1985. FAO species identification sheets for Fishery Purposes. Field guide to the commercial marine and brackish-water species of Pakistan. Prepared with the support of PAK/77/033 and FAO (FIRM) Regular Programme. Rome, FAO, 8p.

Deshmukh, A., Kovale, S., Sawant, M., Shirdhankar, M. and Funde, A., 2010. Reproductive biology of Sardinella longiceps along Ratnagiri coast off Maharashtra. Indian J. mar. Sci., 39: 274-279.

FAO, 2009. Fishery and aquaculture country profile. FAO’s Fisheries Department, Rome, pp. 1-18.

Fox, W.W., 1970. An exponential surplus-yield model for optimizing exploited fish populations. Tans. Am. Fish. Soc., 99: 80-88. https://doi.org/10.1577/1548-8659(1970)99<80:AESMFO>2.0.CO;2

Gabriel, W.L. and Mace, P.M., 1999. A review of biological reference points in the context of the precautionary approach. Proceedings of the fifth national NMFS stock assessment workshop: providing scientific advice to implement the precautionary approach under the Magnuson-Stevens fishery conservation and management act. NOAA Tech Memo NMFS-F/SPO-40: 34-45.

Hilborn, R. and Walters, C.J., 1992. Quantitative fisheries stock assessment, choice, dynamics and uncertainty. Chapman and Hall, New York, London. https://doi.org/10.1007/978-1-4615-3598-0

Hinton, M.G. and Maunder, M.N., 2004. Methods for standardizing CPUE and how to select among them. Col. Vol. Sci. Pap. ICCAT, 56: 169-177.

Hoggarrth, D.D., Abeyasekera, S., Arthur, R.I., Beddington, J.R., Burn, R.W., Halls, A.S, Kirkwood, G.P., McAllister, M., Medley, P., Mees, C.C., Parkes, G.B., Pilling, G.M., Wakeford, R.C. and Welcomme, R.L., 2006. Stock assessment for fishery management-a framework guide to the stock assessment tools of the fisheries management science programme. FAO Fish. Tech. Pap. 487. FAO, Rome, Italy. pp. 261.

Hornell, J., 1924. A contribution to the life-history of the Indian sardine with notes on the plankton of the Malabar coast: Superintendent Government Press.

John, C. and Menon, M., 1942. Food and feeding habits of the oil sardine and mackerel. Curr. Sci., 11: 243-244.

Kalhoro, M.A., Liu, Q., Memon, K.H., Chang, M.S. and Jatt, A.N., 2013. Estimation of maximum sustainable yield of Bombay duck, Harpodon nehereus fishery in Pakistan using the CEDA and ASPIC packages. Pakistan J. Zool., 45: 1757-1764.

Lanier, B.V., 1981. The world supply and demand picture for canned small pelagic fish. Fd and Agric. Org, Food and Agricultural Organization.

Lynch, P.D., Shertzer, K.W. and Latour, R.J., 2012. Performance of methods used to estimate indices of abundance for highly migratory species. Fish. Res., 125: 27-39. https://doi.org/10.1016/j.fishres.2012.02.005

Maunder, M.N., Sibert, J.R., Fonteneau, A., Hampton, J., Kleiber, P. and Harley, S.J., 2006. Interpreting catch per unit effort data assess the status of individual stocks and communities. ICES J. mar. Sci., 63: 1373-1385. https://doi.org/10.1016/j.icesjms.2006.05.008

Musiick, J.A. and Bofnfil, R., 2004. Elasmobranch fisheries management techniques, Fisheries Working Group, Asia-Pacific Economic Cooperation (APEC), Singapore, pp. 133-164.

Nair, R.V., 1949. The growth rings on the otoliths of the oil sardine, Sardinella longiceps Cuv. and Val. Curr. Sci., 18: 9-11.

Niar, R.V., 1959. Notes on the spawning habits and early life-history of the oil sardine, Sardinella longiceps Cuv. and Val. Indian J. Fish., 6: 342-359.

Panwar, S.K., Liu, Q., Khan, F. and Siddiqui, P.J.A., 2012a. Maximum sustainable yield estimates of Ladypees, Sillago sihama (Forsskål), fishery in Pakistan using the ASPIC and CEDA packages. J. Ocean Univ. China, 11: 93-98. https://doi.org/10.1007/s11802-012-1880-3

Panwer, S.K., Liu, Q., Khan, F. and Waryani, B., 2012b. Maximum sustainable yield estimates of spiny lobster fishery in Pakistan using non-equilibrium CEDA package. Russian J. mar. Biol., 38: 448-453. https://doi.org/10.1134/S1063074012060077

Pella, J.J. and Tomlinson, P.K., 1969. A generalized stock production model. Bull. Inter-Am. Trop. Tuna Comm., 13: 421-496.

Pitcher, T.J. and Hart, P.J B., 1982. Fisheries ecology. Kluwer Academic Publishers, the Netherlands, pp. 47.

Prager, M.H., 1994. A suite of extensions to a non-equilibrium surplus-production model. Fish. Bull., 92: 374-389.

Prager, M.H., 2002. Comparison of logistic and generalized surplus production models applied to swordfish Xiphias gladius, in North Atlantic Ocean. Fish. Res., 58: 41-57. https://doi.org/10.1016/S0165-7836(01)00358-7

Prager, M.H., 2005. A stock-production model incorporating covariates (Version 5) and auxiliary programs. CCFHR (NOAA). Miami Laboratory Document MIA-92/93-55, Beaufort Laboratory Document BL-2004-01.

Quinn, II, T.J. and Deriso, R.B., 1999. Quantitative fish dynamics. Oxford University Press, New York, USA, pp. 542.

Schaefer, M.B., 1954. Some aspects of the dynamics of populations important to the management of the commercial marine fisheries. Bull. Inter-Am. Trop. Tuna Comm., 1: 25-56.

Siyal, F.K., Li, Y., Gao, T.X. and Liu, Q., 2013. Maximum sustainable yield estimates of silver pomfret, Pampas argenteus (Family: Strometidae) fishery in Pakistan. Pakistan J. Zool., 45: 447-452.

Small and Medium Enterprise Development Authority (SMEDA), 2015. Government of Pakistan, pp. 30. http://121.52.153.178:8080/xmlui/bitstream/handle/123456789/13129/Fisheries%20Development%20Strategy.pdf?sequence=1&isAllowed=y . Accessed on 2015-11-11.

Smith, T. and Punt, A., 2001. The gospel of maximum sustainable yield in fisheries management: birth, crucifixion and reincarnation. Conservation of exploited species (eds. J.D. Reynolds, G.M. Mace, K.H. Redford, and J.G. Robinson), Cambridge University Press, Cambridge, UK: pp. 41-66.

Sparre, P. and Venema, S.C., 1998. Introduction to tropical fish stock assessment-Part 1: Manual. FAO, 252-253.

Walter, C.J. and Perma, A., 1996. Fixed exploitation rate strategies for copying with effects of climate change. Can. J. Fish. aquat. Sci., 53: 148-158. https://doi.org/10.1139/f95-151

Wang, Y. and Liu, Q., 2013. Applications of CEDA and ASPIC computer packages to the hairtail (Trichiurus japonicus) fishery in the East China Sea. Chinese J. Oceanol. Limnol., 31: 92-96. https://doi.org/10.1007/s00343-013-2073-7

WHO/FAO, 2003. Report of a Joint WHO/FAO Expert Consultation on Diet, nutrition and the prevention of chronic diseases. Wld. Hlth. Organ. Tech. Rep. Ser., 916 (i-viii).